Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H,K lần lượt là hình chiếu của A lên SC, SD. Kí hiệu \(d(A,(SCD))\) là khoảng cách giữa điểm A và mặt phẳng\((SCD)\). Khẳng định nào sau đây đúng:
-
A.
\(d(A,(SCD)) = AC\)
-
B.
\(d(A,(SCD)) = AK\)
-
C.
\(d(A,(SCD)) = AH\)
-
D.
\(d(A,(SCD)) = AD\)
Phương pháp giải
Sử dụng công thức tính khoảng cách từ điểm đến mặt phẳng
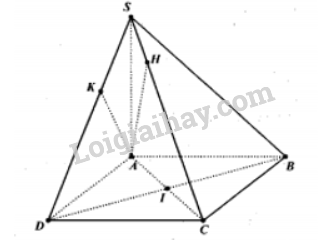
Ta có:
\[\begin{array}{l}\left\{ \begin{array}{l}DC \bot AD\\DC \bot SA\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow DC \bot (SAD) \Rightarrow DC \bot AK\\\left\{ \begin{array}{l}AK \bot SD\\AK \bot DC\\SD,DC \subset (SDC)\\SD \cap DC\end{array} \right. \Rightarrow AK \bot (SDC) \Rightarrow d(A,(SCD)) = AK\end{array}\]
Đáp án A.
Đáp án : A