Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là giao điểm của AC và BD, I là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
-
A.
SI .
-
B.
SO.
-
C.
Đường thẳng qua S vuông góc với SI.
-
D.
Đường thẳng qua S song song với DC.
Phương pháp giải
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là \(d = \left( P \right) \cap \left( Q \right)\).
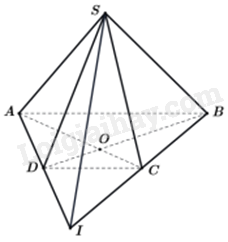
Ta có: S là điểm chung của hai mặt phẳng (SAC) và (SBD).
Vì O là giao điểm của AC và BD nên O là điểm chung của hai mặt phẳng (SAC) và (SBD).
Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
Đáp án : B