Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.
-
A.
\(\left( {AB,SD} \right) = {90^0}\).
-
B.
\(\left( {AB,SD} \right) = {85^0}\).
-
C.
\(\left( {AB,SD} \right) = {70^0}\).
-
D.
\(\left( {AB,SD} \right) = {75^0}\).
Phương pháp giải
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
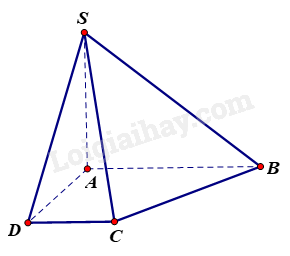
Vì \(SA \bot \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow SA \bot AB\).
Vì ABCD là hình thang vuông tại A nên \(AB \bot AD\).
Ta có: \(AB \bot AD\), \(SA \bot AB\) và SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD)
Do đó, \(AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD\). Suy ra, \(\left( {AB,SD} \right) = {90^0}\).
Đáp án : A