Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\)\(SA \bot (ABCD)\) và \(SA = a.\) Góc giữa đường thẳng \(SB\) và mặt phẳng \((ABCD)\) bằng:
-
A.
\(45^\circ .\)
-
B.
\(90^\circ .\)
-
C.
\(30^\circ .\)
-
D.
\(60^\circ .\)
Phương pháp giải
Sử dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
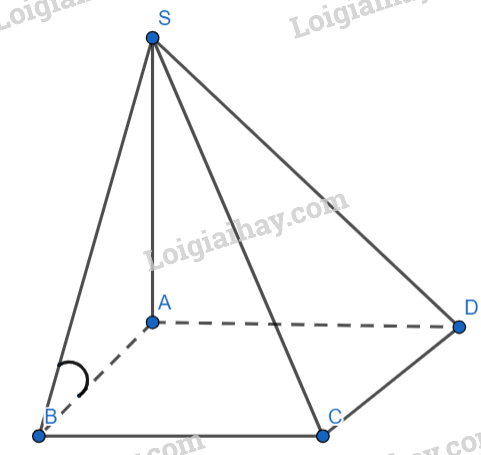
Do \(SA \bot (ABCD)\)
Nên AB là hình chiếu của SA lên mp(ABCD)
Ta có: \(\left( {SB,(ABCD)} \right) = \left( {SB,AB} \right)\)
Xét tam giác SAB vuông tại A ta có:
\(\begin{array}{l}\left( {SB,AB} \right) = \widehat {SBA}\\\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {SBA} = {45^0}\end{array}\)
Đáp án A.
Đáp án : A