Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng — Không quảng cáo

a) \(CD \bot (SHM)\)

b) \(AC \bot (SHM)\)

c) Khoảng cách từ B đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{7}\)

d) Khoảng cách từ O đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{{14}}\)

Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng

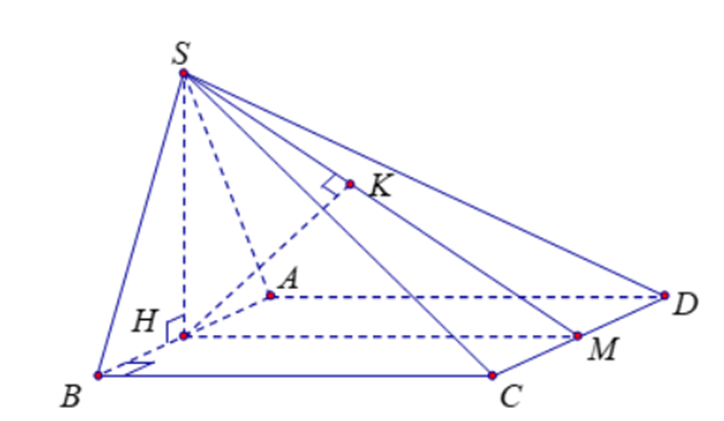
a) \(\left\{ \begin{array}{l}CD \bot HM\\CD \bot SH\\SM,SH \subset (SHM)\\SM \cap SH\end{array} \right. \Rightarrow CD \bot (SHM)\)

b) AC không vuông góc với (SHM)

c) Gọi H, M lần lượt là trung điểm của AB và CD .

Suy ra HM =1, SH = \(\frac{{\sqrt 3 }}{2}\)và SM =\(\frac{{\sqrt 7 }}{2}\)

Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD) nên SH⊥(ABCD)

Vì AB//CD nên AB// (SCD).

Do đó d (B; (SCD)) = d(H; (SCD)) = HK với HK⊥SM trong (SHM).

Ta có:

\(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} \Rightarrow HK = \frac{{\sqrt {21} }}{7}\)

d) \(\begin{array}{l}d(H,(SCD)) = 2.d(O,(SCD))\\ \Rightarrow d(O,(SCD)) = \frac{{\sqrt {21} }}{{14}}\end{array}\)