Cho hình chóp S. ABCD có đáy ABCD là hình vuông, SA vuông — Không quảng cáo

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

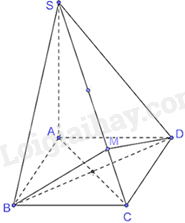
Vì ABCD là hình vuông nên $AC \bot BD$

Vì $SA \bot \left( {ABCD} \right),BD \subset \left( {ABCD} \right) \Rightarrow SA \bot BD$

Ta có: $AC \bot BD$, $SA \bot BD$, SA, AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên $BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC$

Lại có: $BM \bot SC$, BM và BD cắt nhau tại B và nằm trong mặt phẳng (BMD) nên $SC \bot \left( {BMD} \right)$.

Mà $MD \subset \left( {BMD} \right) \Rightarrow MD \bot SC$ hay $MD \bot SM$. Do đó, tam giác SMD vuông tại M.

Đáp án A.