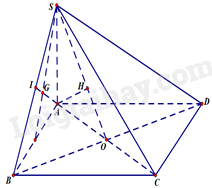
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh 2a. Cạnh bên SA vuông góc với mặt đáy và \(SA = 2a\sqrt 3 \).
a) Chứng minh \(\left( {SAB} \right) \bot \left( {SBC} \right)\), \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
b) Tính góc giữa đường thẳng SC và mặt phẳng \(\left( {SAB} \right)\).
c) Tính góc giữa mặt phẳng \((SBD)\) và mặt phẳng \((ABCD)\).
d) Tính khoảng cách từ \(A\) đến mặt phẳng\(\left( {SBD} \right)\) và khoảng cách từ trọng tâm \(G\) của tam giác SAB đến mặt phẳng \((SBD)\).
a) \(\left\{ {\begin{array}{*{20}{l}}{d \bot \left( P \right)}\\{\left( Q \right) \supset d}\end{array}} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\).
b) Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
c) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến.
d) Sử dụng phương pháp đổi đỉnh.
a) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\\{BC \bot SA{\mkern 1mu} {\mkern 1mu} \left( {SA \bot \left( {ABCD} \right)} \right)}\end{array}} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\).
\(\left\{ {\begin{array}{*{20}{l}}{BD \bot SA{\mkern 1mu} {\mkern 1mu} \left( {SA \bot \left( {ABCD} \right)} \right)}\\{BD \bot AC{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {SBD} \right) \bot \left( {SAC} \right)\).
b) Ta có \(BC \bot \left( {SAB} \right){\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SB} \right)} = \widehat {CSB}\).
Trong tam giác SBC vuông tại \(B\) ta có :
\(\begin{array}{*{20}{l}}{SB = \sqrt {S{A^2} + A{B^2}} {\rm{\;}} = \sqrt {12{a^2} + 4{a^2}} {\rm{\;}} = 4a}\\{BC = 2a \Rightarrow \tan \widehat {CSB} = \frac{{BC}}{{SB}} = \frac{1}{2} \Rightarrow \widehat {CSB} \approx 26^\circ 34'}\end{array}\)
Vậy \(\widehat {\left( {SC;\left( {SAB} \right)} \right)} \approx 26^\circ 34'\).
c) Gọi \(O = AC \cap BD\). Ta có: \(BD \bot \left( {SAC} \right){\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow BD \bot SO\).
\(\left\{ {\begin{array}{*{20}{l}}{\left( {SBD} \right) \cap \left( {ABCD} \right) = BD}\\{\left( {SBD} \right) \supset SO \bot BD}\\{\left( {ABCD} \right) \supset AO \bot BD}\end{array}} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SO;AO} \right)} = \widehat {SOA}\).
ABCD là hình vuông cạnh \(2a \Rightarrow AC = BD = 2a\sqrt 2 {\rm{\;}} \Rightarrow AO = \frac{1}{2}AC = a\sqrt 2 \).
Trong tam giác vuông SAO ta có :
\(SO = \sqrt {S{A^2} + A{O^2}} {\rm{\;}} = \sqrt {12{a^2} + 2{a^2}} {\rm{\;}} = a\sqrt {14} \).
\( \Rightarrow \tan \widehat {SOA} = \frac{{SA}}{{AO}} = \frac{{a\sqrt {14} }}{{a\sqrt 2 }} = \sqrt 7 {\rm{\;}} \Rightarrow \widehat {SOA} \approx 69^\circ 18'\).
Vậy \(\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} \approx 69^\circ 18'\).
d) Trong \(\left( {SAO} \right)\) kẻ \(AH \bot SO{\mkern 1mu} {\mkern 1mu} \left( {H \in SO} \right)\).
Ta có \(BD \bot \left( {SAC} \right) \Rightarrow BD \bot AH\).
\(\left\{ {\begin{array}{*{20}{l}}{AH \bot BD}\\{AH \bot SO}\end{array}} \right. \Rightarrow AH \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AH\).
Áp dụng hệ thức lượng trong tam giác vuông SOA ta có:
\(AH = \frac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \frac{{2a\sqrt 3 .a\sqrt 2 }}{{\sqrt {12{a^2} + 2{a^2}} }} = \frac{{2\sqrt {21} a}}{7}\).
Vậy \(d\left( {A;\left( {SBD} \right)} \right) = \frac{{2\sqrt {21} a}}{7}\).
Trong \(\left( {SAB} \right)\), gọi \(I = AG \cap SB\) ta có: \(AG \cap \left( {SBD} \right) = I\).
\( \Rightarrow \frac{{d\left( {G;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \frac{{GI}}{{AI}} = \frac{1}{3} \Rightarrow d\left( {G;\left( {SBD} \right)} \right) = \frac{1}{3}d\left( {A;\left( {SBD} \right)} \right) = \frac{{2\sqrt {21} a}}{{21}}\).