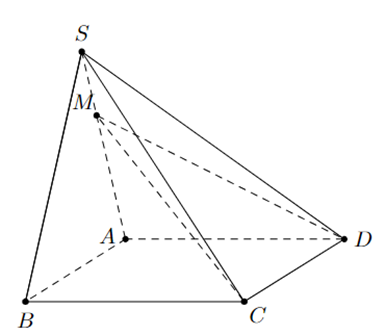
Cho hình chóp S.ABCD có đáy hình bình hành. Trên cạnh SA lấy điểm M sao cho MA = 2MS. Mặt phẳng (CDM) cắt SB tại N. Biết rằng AB = 3 cm, tính tổng MN + CD.
Đáp án:
Đáp án:
- Định lý Thales.
- Quy tắc tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song.
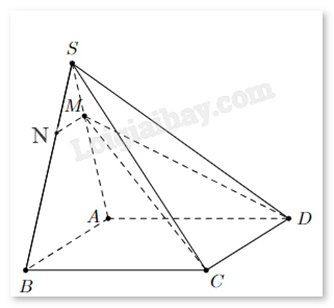
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{M \in (CDM)}\\\begin{array}{l}M \in AB \subset (SAB)\\AB//CD\\AB \subset (SAB),CD \subset (CDM)\end{array}\end{array}} \right.\) nên giao tuyến của (CDM) và (SAB) là đường thẳng d song song với AB, CD và đi qua M.
Giả sử d cắt SA tại N thì đường thẳng MN là giao tuyến của (CDM), (SAB) và MN//AB, suy ra \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{1}{3}\).
Từ đó, dễ dàng chứng minh \(\Delta SMN\)ᔕ\(\Delta SAB\), suy ra \(\frac{{MN}}{{AB}} = \frac{1}{3}\), tức \(MN = \frac{1}{3}AB = \frac{1}{3}.3 = 1\) (cm).
Vì ABCD là hình bình hành nên AB = CD = 3 (cm).
Vậy MN + CD = 1 + 3 = 4 (cm).