Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi O là giao điểm của hai đường chéo, M là trung điểm của SD. Gọi I là điểm thuộc cạnh AB sao cho \(BI = \frac{1}{2}AI\). Giao tuyến của hai mặt phẳng (SAB) và (IOM) là:
-
A.
Đường thẳng qua S song song với MO .
-
B.
Đường thẳng qua I song song với MO.
-
C.
Đường thẳng qua S vuông góc với MO.
-
D.
Đường thẳng qua I vuông góc với MO.
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
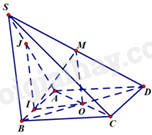
Vì M, O lần lượt là trung điểm của SD, BD nên MO là đường trung bình của tam giác SBD. Do đó, OM // SB.
Mà I là điểm chung của hai mặt phẳng (SAB) và (IOM); \(OM \subset \left( {IOM} \right),SB \subset \left( {SAB} \right)\)
Nên giao tuyến của hai mặt phẳng (SAB) và (IOM) là đường thẳng qua I và song song với OM, cắt SA tại J.
Đáp án : B