Cho hình chóp S. ABCD có đáy là hình vuông tâm O và SA vuông — Không quảng cáo

a) \(CD \bot (SAD)\)

b) \(SC \bot (SAC)\)

c) \(SC \bot HK\)

d) \(HK \bot AI\)

Sử dụng định lý đường thẳng vuông góc với mặt phẳng

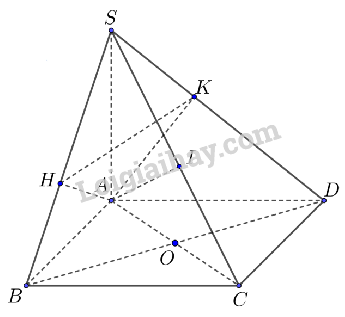
a) Do ABCD là hình vuông nên \(CD \bot AD \subset (SAD)(1)\)

\(SA \bot (ABCD) \Rightarrow SA \bot CD\,(2)\)

Trong (SAD): \(SA \cap AD = A,(3)\)

Từ (1), (2) và (3) nên \(CD \bot (SAD)\)

b) Do ABCD là hình vuông nên \(BD \bot AC\,(4)\)

\(SA \bot (ABCD);BD \subset (ABCD) \Rightarrow SA \bot BD\,\,(5)\)

Trong (SAC): \(SA \cap AC = A,(6)\)

Từ (4), (5) và (6) nên \(BD \bot (SAC)\)

c)Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB,SA \subset (SAB)\end{array} \right. \Rightarrow BC \bot (SAB)\) mà \(AH \subset (SAB) \Rightarrow AH \bot BC\)

Lại có \(AH \bot SB\) nên theo hệ quả, ta được \(AH \bot SC\)

Theo câu (a), \(CD \bot (SAD)\) mà \(AK \subset (SAD)\) nên \(AK \bot CD\)

Lại có AK là đường cao của tam giác \(SAD \Rightarrow AK \bot SD\)

Nên theo hệ quả \(AK \bot SC\)

Trong tam giác AKH: \(AH \bot SC,AK \bot SC\) nên theo hệ quả \(HK \bot SC\)

d)Ta có: \(\Delta SAB = \Delta SAD\,(c.g.c) \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} \Rightarrow HK//BD\,(7)\)

Theo câu (a), \(BD \bot (SAC)\) mà \(AI \subset (SAC) \Rightarrow BD \bot AI\,(8)\)

Từ (7) và (8), \(HK \bot AI\)