Cho hình chóp S. ABCD đáy là hình bình hành, cạnh AB = 6 cm, — Không quảng cáo

Tìm giao điểm của IC với SA, ID với SB. Tìm MN theo định lý Menelaus.

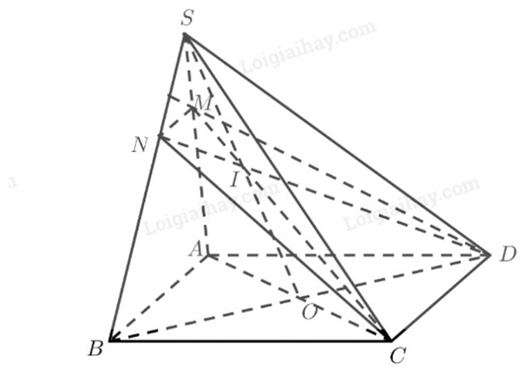
Ta có:

$\left\{ {\begin{array}{*{20}{c}}{M \in (ICD)}\\{M \in SA \subset (SAC)}\end{array}} \right.$ suy ra $M \in (ICD) \cap (SAC)$

$\left\{ {\begin{array}{*{20}{c}}{I \in (ICD)}\\{I \in SO \subset (SAC)}\end{array}} \right.$ suy ra $I \in (ICD) \cap (SAC)$

$C \in (ICD) \cap (SAC)$

Vậy, C, I, M thẳng hàng, tức M là giao điểm của IC và SA.

Chứng minh tương tự, ta có N, I, D thẳng hàng, tức N là giao điểm của ID và SB.

Ta có:$\left\{ {\begin{array}{*{20}{c}}{AB = (SAB) \cap (ABCD)}\\{CD = (ICD) \cap (ABCD)}\\{MN = (SAB) \cap (ICD)}\\{AB//CD}\end{array}} \right.$. Theo định lý về giao tuyến của ba mặt phẳng, ta được: AB//CD//MN.

Áp dụng định lý Menelaus cho $\Delta SAO$ với cát tuyến CIM, ta có:

$\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}$.

Xét $\Delta SAB$ có MN//AB. Theo định lý Thales, ta có: $\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{1}{3} \Leftrightarrow MN = \frac{1}{3}AB = \frac{1}{3}.6 = 2$ (cm).