Đề bài
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\)là hình chữ nhật, \(AD = 2a,AB = 3a\). Cạnh bên \(SA\) vuông góc với đáy, \(SA = 2a\). Khoảng cách giữa hai đường thẳng \(AB\)và \(SD\) bằng
Phương pháp giải
Sử dụng phương pháp xác định khoảng cách giữa hai đường thẳng
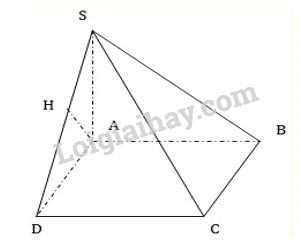
Từ \(A\) kẻ \(AH \bot SD \Rightarrow AH\)là đường vuông góc chung
Chứng minh: Ta có \(AB \bot AH\,\,\left( {Do\,\,AB \bot \left( {SAD} \right)} \right)\)và \(AH \bot SD \Rightarrow AH\)là đường vuông góc chung
\( \Rightarrow d\left( {AB,\,\,SD} \right) = AH.\)
Tính \(AH:\) \(AH = \frac{{AS.AD}}{{\sqrt {A{S^2} + A{D^2}} }} = \frac{{2a.2a}}{{\sqrt {{{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} }} = a\sqrt 2 .\)