Cho hình chóp tam giác đều S.ABC có H là trọng tâm mặt đáy ABC, biết chiều cao hình chóp SH = a, độ dài \(AH = \frac{{a\sqrt 3 }}{3}\), cạnh đáy có độ dài bằng a. Thể tích V của khối chóp S.ABC theo a.
-
A.
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{4}\).
-
B.
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{8}\).
-
C.
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{6}\).
-
D.
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{{12}}\).
Sử dụng kiến thức về hình chóp đều, tính chất đường trung tuyến của tam giác.
B1: Tính chiều cao của cạnh đáy.
B2: Tính diện tích đáy tam giác.
B3: Áp dụng công thức tính thể tích hình chóp đều để tính.
Gọi x là độ dài một cạnh của hình chóp.
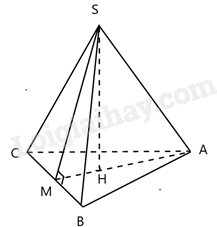
H là trọng tâm tam giác đều ABC, áp dụng tính chất đường trung tuyến trong tam giác ta được:
\(AH = \frac{2}{3}.AM \Rightarrow AM = \frac{{a\sqrt 3 }}{3}:\frac{2}{3} = \frac{{a\sqrt 3 }}{2}\)
Tam giác ABC đều nên diện tích đáy bằng: \(S = \frac{1}{2}.BC.AH = \frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{4}\)
\(V = \frac{1}{3}.S.h = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Đáp án : D