Cho hình chóp tam giác đều S. ABC có tất cả các cạnh bằng — Không quảng cáo

Sử dụng kiến thức về hình chóp đều, độ dài trung đoạn để tính.

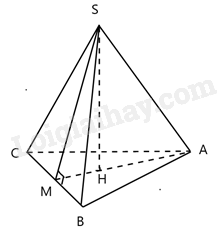
Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau $\Rightarrow SA = SB = SC = AB = AC = BC$.

Gọi H là trọng tâm tam giác ABC đều , M là trung điểm BC.

Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp.

Đáy ABC là tam giác đều $\Rightarrow$AM vừa là trung tuyến vừa là đường cao$\Rightarrow AM \bot BC \Rightarrow \widehat {AMB} = {90^0} \Rightarrow \Delta AMB$vuông tại M.

$AM = 3\sqrt 3 cm$

Ta có: $SA = SB = SC \Rightarrow \Delta SAB$ đều$\Rightarrow$ SM vừa là trung tuyến vừa là đường cao.$\Rightarrow SM \bot BC \Rightarrow \widehat {SMB} = {90^0} \Rightarrow \Delta SMB$ vuông tại M

Xét tam giác vuông SMB và tam giác vuông AMB có:

MB chung

SB = AB

$\Rightarrow \Delta SMB = \Delta AMB$(cạnh huyền – cạnh góc vuông)

$\Rightarrow SM = AM = 3\sqrt 3 (cm)$

Vậy độ dài trung đoạn SM bằng $3\sqrt 3 cm$