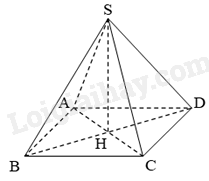
Cho hình chóp tứ giác đều S. ABCD có độ dài tất cả các cạnh — Không quảng cáo

Sử dụng kiến thức về hình chóp đều, chứng minh hai tam giác bằng nhau để so sánh.

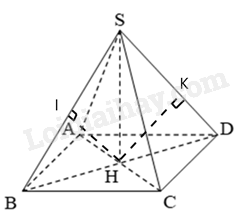
Hình chóp tứ giác đều S.ABC có tất cả các cạnh bằng nhau $\Rightarrow SA = SB = SC = SD = AB = AC = BC = CD$.

Kẻ HI và HK lần lượt vuông góc với SB và SD . Khi đó: ${d_1} = HI,{d_2} = HK$

Xẻ mặt đáy hình chóp là một hình vuông như hình dưới:

Xét tam giác ABH và tam giác CDH có:

AB = CD (ABCD là hình vuông)

${\widehat B_1} = {\widehat D_1}$ (2 góc so le trong)

SB = AB

$\Rightarrow \Delta AHB = \Delta CHD(g.c.g)$

$\Rightarrow BH = DH$(2 cạnh tương ứng)

Xét tam giác SBH và tam giác SHD có:

SB = SD

SH chung

HB = HD ( chứng minh trên)

$\Rightarrow \Delta SHB = \Delta SHD(c.c.c)$

$\Rightarrow \widehat {SBH} = \widehat {SDH}$ (2 góc tương ứng) hay $\widehat {IBH} = \widehat {KDH}$

Xét tam giác vuông IHB và tam giác vuông KHD có:

$\widehat {IBH} = \widehat {KDH}$

HB = HD ( chứng minh trên)

$\Rightarrow \Delta IHB = \Delta KHD$(cạnh huyền – góc nhọn)

$\begin{array}{l} \Rightarrow IH = KH\\ \Rightarrow {d_1} = {d_2}\end{array}$