Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh bằng — Không quảng cáo

Sử dụng kiến thức về hình chóp tứ giác đều, định lý Pythagore và diện tích tam giác đều để tính.

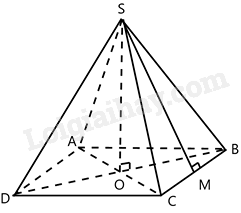
Gọi O là giao hai đường chéo của hình vuông ABCD , M là trung điểm BC.

Khi đó SO là chiều cao của hình chóp.

$AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2$

$AO = \frac{1}{2}.AC = \frac{1}{2}.a\sqrt 2  = \frac{{a\sqrt 2 }}{2}$

$SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{a^2} - {{(\frac{{a\sqrt 2 }}{2})}^2}}  = \frac{{a\sqrt 2 }}{2}$

Đáy ABCD là hình vuông nên diện tích đáy là: ${S_{ABCD}} = a.a = {a^2}$

${V_{ABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}$