Cho hình chóp tứ giác S. ABCD có đáy ABCD là hình thang, AD//BC, \(AD = 2BC\). Gọi O là giao điểm của AC và BD. Gọi G là trọng tâm của tam giác SCD. Chứng minh rằng OG//(SBC).
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với P.
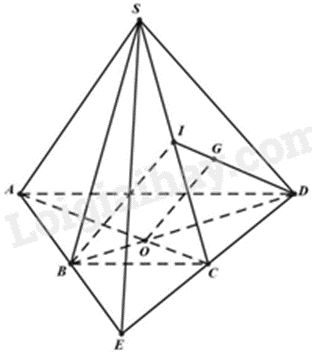
Gọi E là giao điểm của AB và CD.
Vì AD//BC nên $\Delta EBC\backsim \Delta EAD\Rightarrow \frac{EB}{EA}=\frac{EC}{ED}=\frac{BC}{AD}=\frac{1}{2}\Rightarrow EB=\frac{1}{2}EA,EC=\frac{1}{2}ED$
Do đó, B là trung điểm của AE, C là trung điểm của DE.
Suy ra, BD, AC là hai đường trung tuyến của tam giác ADE. Mà O là giao điểm của AC và BD.
Do đó, O là trọng tâm của tam giác ADE. Do đó, \(\frac{{DO}}{{DB}} = \frac{2}{3}\)
Gọi I là trung điểm của SC. Vì G là trọng tâm của tam giác SCD nên \(\frac{{DG}}{{DI}} = \frac{2}{3}\)
Tam giác DIB có: \(\frac{{DG}}{{DI}} = \frac{{DO}}{{DB}} = \frac{2}{3}\) nên OG//IB (định lý Thalès đảo). Mà \(IB \subset \left( {SBC} \right)\) nên OG//(SBC).