Đề bài
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD; EF // AD //BC. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.Tứ giác EMFN là hình gì?
-
A.
Hình bình hành.
-
B.
Hình chữ nhật.
-
C.
Hình thoi.
-
D.
Hình vuông.
Phương pháp giải
Chứng minh tứ giác EMFN là hình chữ nhật có bố cạnh bằng nhau nên tứ giác EMFN là hình vuông.
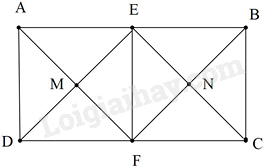
Vì EF // AD //BC
Và AE = FB = BC = CF = FD = DA
Lại có: AE // DF
\( \Rightarrow \)Tứ giác ADFE là hình bình hành (dhnb)
Lại có: \(\widehat A = {90^0}\)( ABCD là hình chữ nhật)
\( \Rightarrow \)Tứ giác ADFE là hình chữ nhật.
Mặt khác: \(AD = AE = \frac{1}{2}AB\)
\( \Rightarrow \) ADFE là hình vuông.
Chứng minh tương tự ta có BCFE là hình vuông
Do đó \(\Delta MEF\) và \(\Delta N{\rm{EF}}\) là hai tam giác vuông cân tại M, N
Suy ra tứ giác EMFN là hình vuông.
Đáp án : D