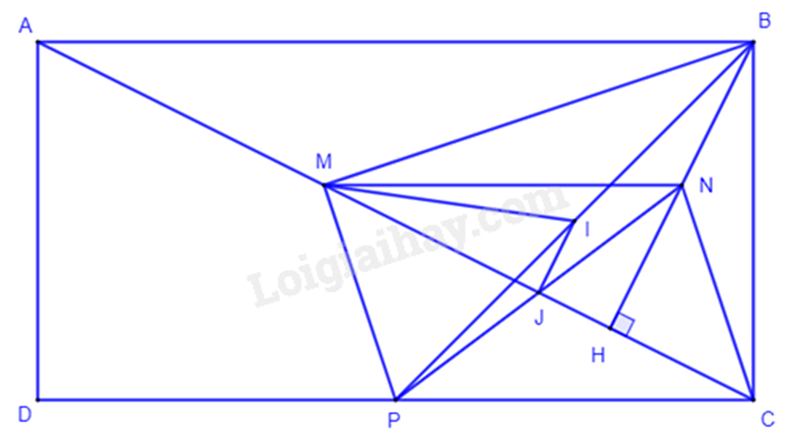
Cho hình chữ nhật ABCD có AB = 2AD. Vẽ BH vuông góc với AC . Gọi M, N, P lần lượt là trung điểm của AH, BH, CD.
a) Chứng minh tứ giác MNCP là hình bình hành.
b) Chứng minh MP vuông góc MB.
c) Gọi I là trung điểm của BP và J là giao điểm của MC và NP. Chứng minh rằng: MI – IJ < JP
a) Chứng minh tứ giác MNCP có hai cạnh đối song song và bằng nhau.
b) Chứng minh N là trực tâm của tam giác CMB nên NC\( \bot \)MB\( \Rightarrow \) MP\( \bot \)MB (MP // CN).
c) Chứng minh MI = PI, sử dụng bất đẳng thức tam giác để chứng minh PI – IJ < JP hay MI – IJ < JP.
a) Xét tam giác AHB có:
M là trung điểm của AH
N là trung điểm của BH
=> MN là đường trung bình của tam giác AHB => MN // AB và MN = \(\frac{1}{2}\)AB.
Vì P là trung điểm của CD nên CP = PD = \(\frac{1}{2}\)CD.
Mà AB // CD; AB = CD (ABCD là hình chữ nhật) => CP = \(\frac{1}{2}\)AB.
=> MN // CP (cùng song song với AB) và MN = CP (\(\frac{1}{2}\)AB).
Do đó tứ giác MNCP là hình bình hành (đpcm)
b) Do MN // AB (cmt) mà AB \( \bot \) BC (ABCD là hình chữ nhật) nên MN \( \bot \) BC.
Ta có BH \( \bot \) MC (gt)
Mà MN \( \cap \) BH tại N.
=> N là trực tâm của tam giác CMB suy ra CN \( \bot \) BM.
Mà CN // PM (MNCP là hình bình hành)
=> PM \( \bot \) BM (đpcm)
c) Xét tam giác PMB vuông tại M có I là trung điểm của BP nên MI là đường trung tuyến ứng với cạnh huyền của tam giác PMB => MI = \(\frac{1}{2}\)BP = PI.
Xét tam giác PIJ, ta có: PI – IJ < JP hay MI – IJ < JP (đpcm).