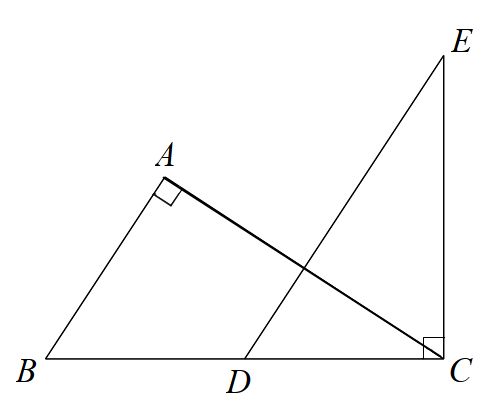
Cho hình dưới đây. Biết AB // DE. Chọn hệ thức sai trong — Không quảng cáo

Dựa vào AB // DE suy ra $\widehat {ABC} = \widehat {EDC}$.

Chứng minh $\Delta ABC\backsim \Delta CDE\left( g.g \right)$ suy ra tỉ số giữa các cặp cạnh tương ứng.

Vì AB // DE nên $\widehat {ABC} = \widehat {EDC}$ (hai góc đồng vị)

Xẻ $\Delta ABC$ và $\Delta CDE$ có:

$\widehat A = \widehat C\left( { = {{90}^0}} \right)$

$\widehat {ABC} = \widehat {EDC}$ (cmt)

Suy ra $\Delta ABC\backsim \Delta CDE\left( g.g \right)$. Từ đó ta được:

$\frac{{AB}}{{AC}} = \frac{{CD}}{{CE}}$ suy ra $AB.CE = AC.CD$. (A đúng)

$\frac{{AB}}{{BC}} = \frac{{CD}}{{DE}}$ suy ra $AB.DE = BC.CD$ (B đúng)

$\frac{{AC}}{{BC}} = \frac{{CE}}{{DE}}$ suy ra $AC.DE = CE.BC$ (C đúng)

Vậy D sai (vì không có tỉ lệ nào suy ra $AB.AC = DE.DC$).

Đáp án D.