Cho hình hộp ABCD.A’B’C’D’.
a) Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \)
b) Vecto đối của vecto \(\overrightarrow {A'A} \) là \(\overrightarrow {B'B} \)
c) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {A'B'} \)
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {C'A} \)
a) Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \)
b) Vecto đối của vecto \(\overrightarrow {A'A} \) là \(\overrightarrow {B'B} \)
c) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {A'B'} \)
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {C'A} \)
Sử dụng các quy tắc cộng, trừ vecto và lý thuyết các vecto bằng nhau, các vecto đối nhau.
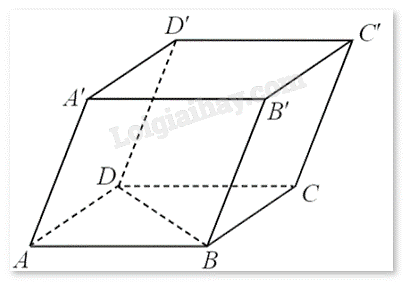
a) Đúng. Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \) vì chúng cùng phương, cùng chiều và cùng độ dài.
b) Sai. Hai vecto \(\overrightarrow {A'A} \),\(\overrightarrow {B'B} \) cùng chiều nên không phải vecto đối nhau.
c) Đúng. Vì \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {AB} = 2\overrightarrow {A'B'} \) .
d) Sai. Vì \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {CC'} - \overrightarrow {CA} = \overrightarrow {AC'} \) .