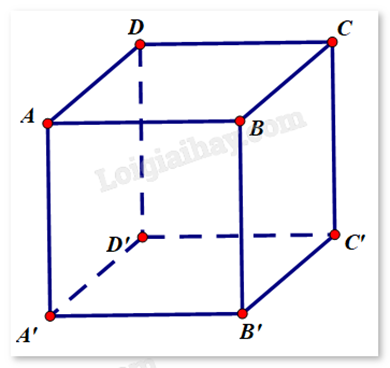
Cho hình hộp ABCD. A’B’C’D’ tâm — Không quảng cáo

a) $\overrightarrow {AB}  + \overrightarrow {AA'}  = \overrightarrow {AD}  + \overrightarrow {DD'}$

b) $\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}$

c) $\overrightarrow {AB}  + \overrightarrow {BC'}  + \overrightarrow {CD}  + \overrightarrow {D'A}  = \overrightarrow 0$

d) $\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CC'}  = \overrightarrow {AD'}  + \overrightarrow {D'O}  + \overrightarrow {OC'}$

Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc ba điểm, quy tắc hình hộp.

a) Sai . $\overrightarrow {AB}  + \overrightarrow {AA'}  = \overrightarrow {AB'}$, $\overrightarrow {AD}  + \overrightarrow {DD'}  = \overrightarrow {AD'}$, mà $\overrightarrow {AB'}  \ne \overrightarrow {AD'}$ nên $\overrightarrow {AB}  + \overrightarrow {AA'}  = \overrightarrow {AD}  + \overrightarrow {DD'}$ sai.

b) Đúng. Theo quy tắc hình hộp: $\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}$.

c) Đúng . $(\overrightarrow {AB}  + \overrightarrow {CD} ) + (\overrightarrow {BC'}  + \overrightarrow {D'A} ) = \overrightarrow 0  \Leftrightarrow \overrightarrow 0  + \overrightarrow 0  = \overrightarrow 0$.

d) Đúng. $\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CC'}  = \overrightarrow {AC'}$, $\overrightarrow {AD'}  + \overrightarrow {D'O}  + \overrightarrow {OC'}  = \overrightarrow {AC'}$, suy ra $\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CC'}  = \overrightarrow {AD'}  + \overrightarrow {D'O}  + \overrightarrow {OC'}$.