Đề bài
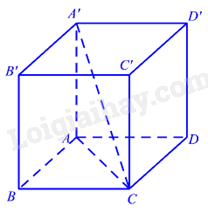
Cho hình hộp chữ nhật ABCD.A'B'C'D' có \(AB = BC = a,{\mkern 1mu} AA' = \sqrt 6 a\) (tham khảo hình dưới). Góc giữa đường thẳng A'C và mặt phẳng \(\left( {ABCD} \right)\) bằng:
-
A.
\(60^\circ \).
-
B.
\(90^\circ \).
-
C.
\(30^\circ \).
-
D.
\(45^\circ \).
Phương pháp giải
\(\left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\)
Ta có \(\left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\)
Ta có \(AC = \sqrt {A{B^2} + B{C^2}} {\rm{ \;}} = a\sqrt 2 \).
Xét tam giác \(\Delta A'CA\) có \(\tan \widehat {A'CA} = \frac{{A'A}}{{AC}} = \frac{{\sqrt 6 a}}{{\sqrt 2 a}} = \sqrt 3 {\rm{ \;}} \Rightarrow \widehat {A'CA} = {60^\circ }\).
Vậy góc A'C và mặt phẳng \(\left( {ABCD} \right)\) và bằng \(60^\circ \).
Đáp án A.
Đáp án : A