Cho hình khối chóp tam giác đều S. ABC có cạnh đáy bằng a — Không quảng cáo

Sử dụng tính chất đường trung bình.

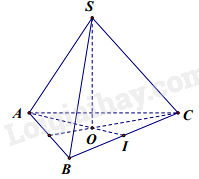
Gọi I là trung điểm của cạnh BC, vì tam giác ABC là tam giác đều nên AI là đường trung tuyến đồng thời là đường cao của tam giác ABC.

Áp dụng định lí Pythagore vào tam giác ABI, ta có:

\(\begin{array}{l}A{I^2} = A{B^2} - B{I^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\\ \Rightarrow AI = \sqrt {\frac{{3{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\end{array}\)\(\)

\(AO = \frac{2}{3}AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\) (O là trọng tâm)

Áp dụng định lí Pythagore vào tam giác SOA, ta có:

\(\begin{array}{l}S{O^2} = S{A^2} - A{O^2} = {\left( {2a} \right)^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = \frac{{11{a^2}}}{3}\\ \Rightarrow SO = \sqrt {\frac{{11{a^2}}}{3}} = \frac{{a\sqrt {33} }}{3}\end{array}\)

Vậy thể tích khối chóp S.ABC là:

\(\begin{array}{l}V = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {33} }}{3}\left( {\frac{1}{2}\frac{{a\sqrt 3 }}{2}.a} \right)\\ = \frac{{{a^3}\sqrt {11} }}{{12}}\end{array}\)