Đề bài
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng \(\left( {A'BC} \right)\) tạo với đáy một góc bằng \({60^\circ }.\) Thể tích khối lăng trụ ABC.A'B'C' bằng:
-
A.
\(\frac{{\sqrt 3 {a^3}}}{8} \cdot \)
-
B.
\(\frac{{3\sqrt 3 {a^3}}}{8} \cdot \)
-
C.
\(\frac{{\sqrt 3 {a^3}}}{2} \cdot \)
-
D.
\(\frac{{3\sqrt 3 {a^3}}}{4} \cdot \)
Phương pháp giải
\(V = AA'.{S_{ABC}}\)
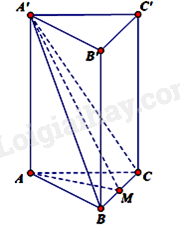
\( \Rightarrow \left( {A'AM} \right) \bot BC \Rightarrow A'M \bot BC\)
Do đó, \(\widehat {A'AM} = \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = {60^o}\).
Dễ thấy \(A'A = AM.\tan {60^o} = \frac{{a\sqrt 3 }}{2}.\sqrt 3 {\rm{ \;}} = \frac{{3a}}{2}\).
Do đó, thể tích đa diện là \(V = AA'.{S_{ABC}} = \frac{{3a}}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}\sqrt 3 }}{8}\).
Đáp án B.
Đáp án : B