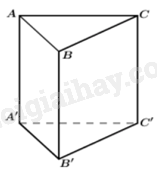
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng nhau. Gọi \(\alpha \) là góc tạo bởi hai đường thẳng B'C và AB. Tính cosin của góc \(\alpha \).
-
A.
\(\cos \alpha {\rm{ \;}} = \frac{{\sqrt 3 }}{6}\)
-
B.
\(\cos \alpha {\rm{ \;}} = \frac{{\sqrt 2 }}{4}\)
-
C.
\(\cos \alpha {\rm{ \;}} = {\rm{ \;}} - \frac{{\sqrt 3 }}{4}\)
-
D.
\(\cos \alpha {\rm{ \;}} = \frac{{\sqrt 2 }}{2}\)
- Sử dụng \(a//a' \Rightarrow \widehat {\left( {a;b} \right)} = \widehat {\left( {a';b} \right)}\).
- Sử dụng định lí cosin trong tam giác.
Ta có \(AB//A'B'\) nên \(\widehat {\left( {B'C;AB} \right)} = \widehat {\left( {B'C;A'B'} \right)}\).
Ta có: \(A'C = B'C = a\sqrt 2 \) (do \(ACC'A',{\mkern 1mu} {\mkern 1mu} BCC'B'\) là các hình vuông cạnh \(a\)).
Áp dụng định lí Cosin trong tam giác A'B'C ta có:
\(\cos \widehat {A'B'C} = {\rm{ }}\frac{{A'{B^2} + B'{C^2} - A'{C^2}}}{{2A'B'.B'C}} = \frac{{{a^2} + 2{a^2} - 2{a^2}}}{{2a.a\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\)
Vậy \(\cos \left( {B'C;AB} \right) = \frac{{\sqrt 2 }}{4}\).
Đáp án B.
Đáp án : B