Cho hình lập phương ABCD cdot A'B'C'D' cạnh a. I là trung

Đề bài

Cho hình lập phương $ABCD \cdot A'B'C'D'$ cạnh $a$ . I là trung điểm CD'. Khoảng cách từ $I$ dến mặt phằng $\left( {BDD'B'} \right)$ bằng

A.
$\frac{{a\sqrt 2 }}{4}$ .
B.
$\frac{a}{4}$ .
C.
$\frac{{a\sqrt 6 }}{4}$ .
D.
$\frac{{a\sqrt 3 }}{4}$ .

Phương pháp giải

Đưa về khoảng cách từ C’ đến (BDD’B’)

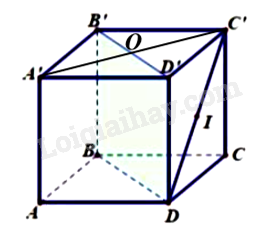
Mà $A'C' \bot B'D' \Rightarrow A'C' \bot \left( {BDD'B'} \right)$

$\begin{array}{*{20}{l}}{ \Rightarrow d\left( {C';\left( {BDD'B'} \right)} \right) = C'O}\\{C'O = \frac{1}{2}A'C' = \frac{1}{2}\sqrt {2{a^2}} {\rm{ \;}} = \frac{{a\sqrt 2 }}{2}}\\{ \Rightarrow d\left( {I;\left( {BDD'B'} \right)} \right) = \frac{{a\sqrt 2 }}{4}}\end{array}$

Đáp án A.

Đáp án : A