Đề bài
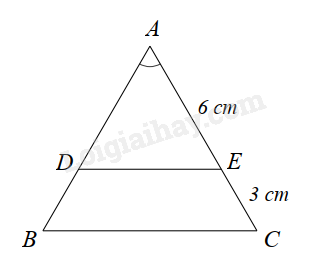
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân.
Chọn kết luận đúng trong các câu sau:
-
A.
$\Delta ADE\backsim \Delta ABC\left( g.g \right)$ với $k=2$.
-
B.
$\Delta ADE\backsim \Delta ABC\left( c.c.c \right)$ với $k=\frac{2}{3}$.
-
C.
$\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$ với $k=\frac{3}{2}$.
-
D.
$\Delta ABC\backsim \Delta ADE\left( g.g \right)$ với $k=\frac{1}{2}$.
Phương pháp giải
Chứng minh $\Delta ADE\backsim \Delta ABC$ theo trường hợp cạnh – góc – cạnh.
Vì \(\Delta ABC,\Delta ADE\) cân nên \(AB = AC\); \(AD = AE\left( { = 6cm} \right)\).
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat A\) chung
\(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\) (vì \(AB = AC;AD = AE\))
suy ra $\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$
suy ra \(k = \frac{{AC}}{{AE}} = \frac{{AE + EC}}{{AE}} = \frac{{6 + 3}}{6} = \frac{9}{6} = \frac{3}{2}\).
Đáp án C.
Đáp án : C