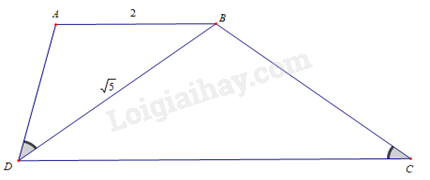
Cho hình thang ABCD,,AB,//,CD, góc ADB = góc BCD, AB =

Đề bài

Cho hình thang $ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)$ , $\widehat {ADB} = \widehat {BCD}$ , $AB = 2\,{\rm{cm}}$ , $BD = \sqrt 5 \,{\rm{cm}}$ . Độ dài đoạn thẳng $CD$ là

A.
$2\sqrt 5 \,{\rm{cm}}$ .
B.
$\sqrt 5 - 2\,{\rm{cm}}$ .
C.
$\frac{{\sqrt 5 }}{2}\,{\rm{cm}}$ .
D.
$2,5\,{\rm{cm}}$ .

Phương pháp giải

Chứng minh

$\Delta \,ADB\,\, \backsim \Delta BCD$ (g – g ) nên suy ra tỉ số các cạnh tương ứng từ đó tính độ dài cạnh CD.

Vì $AB\,{\rm{//}}\,CD \Rightarrow \widehat {ABD} = \widehat {BDC}$ (cặp góc so le trong).

Xét $\Delta \,ADB$ và $\Delta \,BCD$ có:

$\widehat {ABD} = \widehat {BDC}$ (chứng minh trên); $\widehat {ADB} = \widehat {BCD}$ (gt)

Nên $\Delta \,ADB\, \backsim \Delta BCD$ (g – g ).

$\Rightarrow \frac{{AB}}{{BD}} = \frac{{DB}}{{CD}} \Leftrightarrow \frac{2}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{{CD}} \Leftrightarrow CD = \frac{{\sqrt 5 .\sqrt 5 }}{2} = \frac{5}{2} = 2,5\,\,\left( {{\rm{cm}}} \right)$ .

Đáp án : D