Cho hình thang ABCD AB // CD. Gọi giao điểm hai đường chéo — Không quảng cáo

Phương pháp giải

a) Sử dụng hệ quả của định lí Thales trong tam giác để tính CD.

b) Áp dụng định lí Thales để tính OH.

Sử dụng công thức tính diện tích tam giác.

c) Dựa vào hệ quả và định lí Thales để chứng minh.

d) Chứng minh $\frac{{AE}}{{AD}} = \frac{{BF}}{{BC}}$ để suy ra $\frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = 1$.

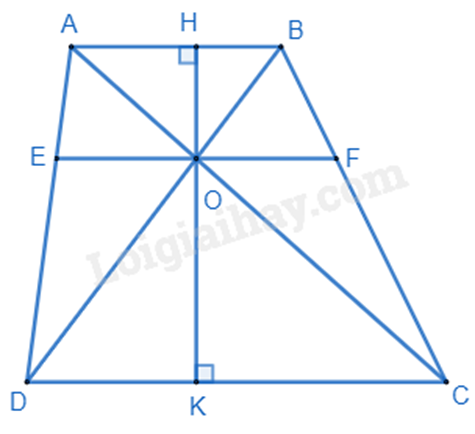
a) Xét tam giác OCD có AB // CD, ta có:

$\frac{{AO}}{{OC}} = \frac{{AB}}{{CD}}$ (hệ quả của định lí Thales)

$\frac{4}{8} = \frac{5}{{CD}} \Rightarrow CD = 5:\frac{4}{8} = 10\left( {cm} \right)$

b) Xét tam giác OKC có AH // KC (vì AB // CD), ta có:

$\frac{{HO}}{{OK}} = \frac{{OA}}{{OC}}$ (Định lí Thales)

$\begin{array}{l}\frac{{OH}}{6} = \frac{4}{8} = \frac{1}{2}\\ \Rightarrow OH = \frac{1}{2}.6 = 3\left( {cm} \right)\end{array}$

$\Rightarrow {S_{\Delta AOB}} = \frac{1}{2}OH.AB = \frac{1}{2}3.5 = 7,5\left( {c{m^2}} \right)$

c) Xét tam giác ACD có EO // CD (vì AB // CD) nên $\frac{{EO}}{{CD}} = \frac{{AO}}{{AC}}$ (hệ quả của định lí Thales)

Xét tam giác BCD có OF // CD (vì AB // CD) nên $\frac{{BF}}{{BC}} = \frac{{OF}}{{CD}}$ (hệ quả của định lí Thales)

Xét tam giác ABC có OF // AB nên $\frac{{AO}}{{AC}} = \frac{{BF}}{{BC}}$ (định lí Thales) (1)

$\Rightarrow \frac{{EO}}{{CD}} = \frac{{OF}}{{CD}} \Rightarrow EO = OF$ (đpcm)

d) Xét tam giác ACD có EO // CD nên $\frac{{AE}}{{AD}} = \frac{{AO}}{{AC}}$ (2)

Từ (1) và (2) suy ra $\frac{{AE}}{{AD}} = \frac{{BF}}{{BC}}$

$\Rightarrow \frac{{AE}}{{AD}} + \frac{{CF}}{{BC}} = \frac{{BF}}{{BC}} + \frac{{CF}}{{BC}} = \frac{{BF + CF}}{{BC}} = \frac{{BC}}{{BC}} = 1$ (đpcm).