Đề bài
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O cho \(OA = OB\); \(OC = OD\). Khẳng định nào sau đây là sai?
-
A.
ABCD là hình thang cân.
-
B.
AC = BD.
-
C.
BC = AD.
-
D.
Tam giác AOD cân tại O.
Phương pháp giải
Dựa vào đặc điểm của hình thang cân.
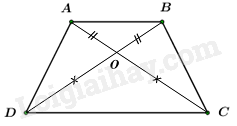
Vì OA = OB và OC = OD nên AC = BD hay hai đường chéo bằng nhau, khẳng định B đúng.
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân, khẳng định A đúng.
Hình thang ABCD cân nên BC = AD (hai cạnh bên bằng nhau), khẳng định C đúng.
Vì chưa đủ điều kiện để chứng minh AOD cân tại O nên khẳng định D sai.
Đáp án D.
Đáp án : D