Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và — Không quảng cáo

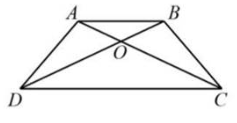
Ta có ${S_{CAB}} = {S_{DAB}}$ (Hai tam giác có chung đáy AB và chiều cao hạ từ D xuống AB bằng chiều cao hạ từ C xuống AB)

Mà ${S_{DAB}} = {S_{OAB}} + {S_{OAD}} = 5 + 11 = 16$ (cm ² ) nên ${S_{CAB}} = 16c{m^2}$

$\Rightarrow {S_{OBC}} = {S_{CAB}} - {S_{OAB}} = 16 - 5 = 11$ (cm ² )

Xét tam giác AOB và AOD có $\frac{{{S_{AOB}}}}{{{S_{AOD}}}} = \frac{{OB}}{{OD}} = \frac{5}{{11}}$ (chung chiều cao hạ từ A xuống BD nên tỉ số diện tích bằng tỉ số hai đáy)

Xét tam giác OBC và ODC có $\frac{{{S_{OBC}}}}{{{S_{OCD}}}} = \frac{{OB}}{{OD}} \Rightarrow \frac{{11}}{{{S_{ODC}}}} = \frac{5}{{11}}$

Suy ra ${S_{ODC}} = \frac{{11 \times 11}}{{15}} = 24,2$ (cm ² )

Vậy ${S_{ABCD}} = {S_{ABD}} + {S_{OBC}} + {S_{ODC}} = 16 + 11 + 24,2 = 51,2$ (cm ² )