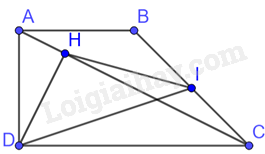
Cho hình thang ABCD vuông tại A và D. Biết CD = 2AB = 2AD — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ hai của tam giác vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.

Áp dụng định lý Pythagore vào tam giác ADB vuông tại A có: \(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow BD = a\sqrt 2 \)

Tam giác ABD vuông cân tại A nên \(\widehat {ADB} = {45^0}\)

Ta có: \(B{D^2} + B{C^2} = 2{a^2} + 2{a^2} = 4{a^2} = C{D^2}\) nên tam giác BDC vuông tại B, do đó, \(\widehat {DBC} = {90^0}\)

Xét tam giác ADC và tam giác IBD có:

\(\widehat {ADC} = \widehat {IBD} = {90^0},\frac{{AD}}{{IB}} = \frac{{DC}}{{BD}}\)

Do đó, \(\Delta ADC \backsim \Delta IBD\)

Suy ra, \(\widehat {ACD} = \widehat {BDI}\)

Mà \(\widehat {ADH} = \widehat {ACD}\) (cùng phụ với góc HDC)

Do đó, \(\widehat {ADH} = \widehat {BDI}\)

Mà \(\widehat {ADH} + \widehat {BDH} = {45^0} \Rightarrow \widehat {BDI} + \widehat {BDH} = {45^0}\) hay \(\widehat {HDI} = {45^0}\)