Cho hình thang \(ABCD\left( {AB // CD} \right)\) có diện tích \(48\,{\rm{c}}{{\rm{m}}^2}\) , \(AB = 4\,{\rm{cm,}}\,CD = 8{\rm{cm}}\) . Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\)
-
A.
\(\frac{{64}}{3}{\rm{c}}{{\rm{m}}^2}\)
-
B.
\({\rm{15c}}{{\rm{m}}^2}\)
-
C.
\({\rm{16c}}{{\rm{m}}^2}\)
-
D.
\({\rm{32c}}{{\rm{m}}^2}\)
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
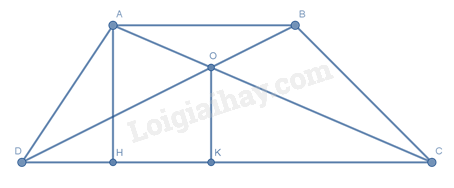
Kẻ \(AH \bot DC;\,OK \bot DC\) tại \(H,\,K\) \( \Rightarrow AH \bot OK\) .
Chiều cao của hình thang \(AH = \frac{{2{S_{ABCD}}}}{{AB + CD}} = \frac{{2.48}}{{4 + 8}} = 8\) (cm)
Vì \(AB // CD\) ( \(ABCD\) là hình thang) nên theo hệ quả định lí Thalès ta có \(\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{8}{4} = 2\)
\(\begin{array}{l} \Rightarrow \frac{{OC}}{{OA + OC}} = \frac{2}{{2 + 1}}\\ \Rightarrow \frac{{OC}}{{AC}} = \frac{2}{3}\end{array}\)
Vì \(AH // OK\) nên theo hệ quả định lý Thalès ta có \(\frac{{OK}}{{AH}} = \frac{{OC}}{{AC}} = \frac{2}{3} \Rightarrow OK = \frac{2}{3}AH = \frac{2}{3} \cdot 8 = \frac{{16}}{3}\) (cm)
Do đó \({S_{COD}} = \frac{1}{2}OK.DC = \frac{1}{2} \cdot \frac{{16}}{3} \cdot 8 = \frac{{64}}{3}\,{\rm{c}}{{\rm{m}}^2}\) .
Đáp án : A