Cho hình thang MNPQ MN // PQ, đường cao ME. Hình thang MNPQ — Không quảng cáo

Phương pháp giải

a) Sử dụng công thức tính diện tích hình thang để suy ra đường cao ME.

b) Sử dụng hệ quả của định lí Thales để chứng minh.

c) Sử dụng hệ quả của định lí Thales để tính IF. Sử dụng công thức tính diện tích tam giác.

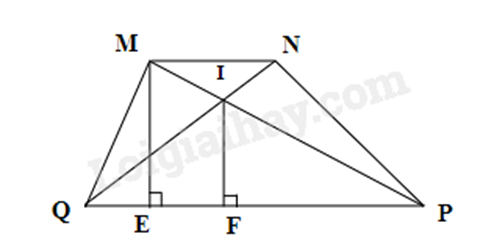
a) Ta có:

$\begin{array}{l}{S_{MNPQ}} = \frac{1}{2}\left( {MN + PQ} \right).ME\\ \Rightarrow ME = \frac{{2{S_{MNPQ}}}}{{MN + PQ}} = \frac{{2.36}}{{4 + 8}} = 6\left( {cm} \right)\end{array}$

b) Xét $\Delta IPQ$ có MN // PQ nên $\frac{{IP}}{{IM}} = \frac{{PQ}}{{MN}} \Rightarrow \frac{{IP}}{{IM}} = \frac{8}{4} = 2$ (hệ quả của định lí Thales)

$\begin{array}{l} \Rightarrow \frac{{IP}}{{IP + IM}} = \frac{2}{{2 + 1}}\\ \Rightarrow \frac{{IP}}{{MP}} = \frac{2}{3}\end{array}$

$\Rightarrow IP = \frac{2}{3}MP$ (đpcm)

c) Kẻ $IF \bot PQ$, mà $ME \bot PQ$ $\Rightarrow IF//ME$

Do $\Delta PME$ có $IF//ME$ nên $\frac{{IF}}{{ME}} = \frac{{IP}}{{MP}} = \frac{2}{3}$

$\Rightarrow IF = \frac{2}{3}ME \Rightarrow IF = \frac{2}{3}.6 = 4\left( {cm} \right)$

$\Rightarrow {S_{\Delta IPQ}} = \frac{{IF.PQ}}{2} = \frac{{4.8}}{2} = 16\left( {c{m^2}} \right)$