Đề bài
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
-
A.
\(AC = BD\).
-
B.
Tứ giác \(ABCD\) là hình chữ nhật.
-
C.
\(M\) là trung điểm của \(BD\).
-
D.
\(AB = AD\).
Phương pháp giải
Sử dụng tính chất của hình chữ nhật
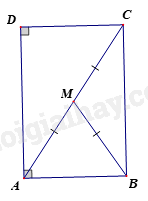
Xét \(\Delta ABC\) có \(BM\) là đường trung tuyến ứng với cạnh \(AC\) mà \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\)\( \Rightarrow \Delta ABC\) vuông tại \(B\)
Tứ giác \(ABCD\) có \(\widehat A = \widehat D = \widehat B = {90^o}\)\( \Rightarrow \) Tứ giác \(ABCD\) là hình chữ nhật.
Suy ra: \(AC = BD\) và \(M\) là trung điểm của \(BD\)
Vậy D sai.
Đáp án : D