Cho hình thang vuông ABCD, góc A = góc D = 90^0 có AB = — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ hai của tam giác vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.

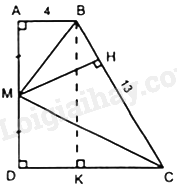
Kẻ BK vuông góc với CD tại K.

Tứ giác ABKD có: $\widehat A = \widehat D = \widehat {BKD} = {90^0}$ nên tứ giác ABKD là hình chữ nhật, do đó, $KC = DC - DK = 5cm$

Áp dụng định lý Pythagore vào tam giác BKC vuông tại K ta có:

$B{C^2} = C{K^2} + K{B^2} \Rightarrow K{B^2} = 144 \Rightarrow KB = 12cm$

Vì tứ giác ABKD là hình chữ nhật nên $AD = BK = 12cm$ do đó $AM = MD = 6cm$

Xét tam giác ABM và tam giác DMC có:

$\widehat {BAM} = \widehat {MDC} = {90^0},\frac{{AB}}{{DM}} = \frac{{AM}}{{DC}}\left( { = \frac{2}{3}} \right)$

Do đó, $\Delta ABM \backsim \Delta DMC$

Suy ra, $\widehat {AMB} = \widehat {DCM}$

Mà $\widehat {DMC} + \widehat {MCD} = {90^0} \Rightarrow \widehat {DMC} + \widehat {AMB} = {90^0}$

Ta có: $\widehat {DMC} + \widehat {BMC} + \widehat {AMB} = {180^0} \Rightarrow \widehat {BMC} = {90^0}$

Do đó, tam giác BMC vuông tại M.

Kẻ MH vuông góc với BC tại H thì MH là khoảng cách từ M đến BC.

Áp dụng định lý Pythagore vào hai tam giác ABM và tam giác DMC ta được:

$\left\{ \begin{array}{l}B{M^2} = M{A^2} + A{B^2} = {6^2} + {4^2} = 52\\M{C^2} = C{D^2} + D{M^2} = {9^2} + {6^2} = 117\end{array} \right.$

Do đó, $BM = 2\sqrt {13} cm,MC = 3\sqrt {13} cm$

Diện tích tam giác BMC vuông tại M có:

$\frac{1}{2}BM.MC = \frac{1}{2}MH.BC \Rightarrow 2\sqrt {13} .3\sqrt {13}  = 13.MH \Rightarrow MH = 6cm$