Đề bài
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Phương pháp giải
Chứng minh \(\Delta \,ABD\,\, \backsim \Delta BDC\) (g – g) nên suy ra tỉ số các cạnh tương ứng và độ dài của cạnh BD.
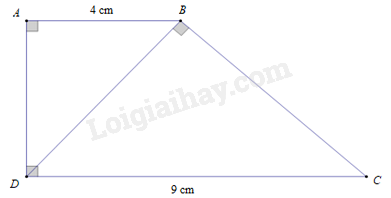
Ta có \(AB\,{\rm{//}}\,{\rm{CD}}\) ( vì cùng vuông góc với \(A{\rm{D}}\)).\( \Rightarrow \widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(\Delta ABD\) và \(\Delta BDC\) có:
\(\widehat {BAD} = \widehat {DBC} = 90^\circ \); \(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Nên \(\Delta \,ABD\,\, \backsim \,\Delta BDC\) (g – g) \( \Rightarrow \frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} \Rightarrow B{D^2} = AB.DC = 4.9 = 36 \Rightarrow BD = 6\,\,\left( {{\rm{cm}}} \right)\).
Đáp án : D