Cho hình thang vuông ABCD hat A = hat D = 90^0 có AB = 4cm, — Không quảng cáo

Phương pháp giải

Chứng minh \(\Delta AMB \backsim \Delta DCM(c - g - c)\) suy ra số đo góc BMC.

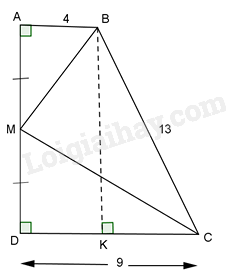
Kẻ \(BK \bot CD(K \in CD)\) thì tứ giác ABKD là hình có 3 góc vuông nên nó là hình chữ nhật.

Do đó: \(DK = AB = 4(cm) \Rightarrow KC = DC - DK = 9 - 4 = 5(cm)\)

Tam giác KBC vuông tại K, theo định lý Pytago ta có:

\(B{C^2} = C{K^2} + K{B^2}\) hay \({13^2} = {5^2} + K{B^2} \Rightarrow KB = 12(cm)\) nên \( \Rightarrow AD = KB = 12(cm)\)

M là trung điểm của AD nên \(AM = MD = \frac{1}{2}AD = 6(cm)\)

Xét \(\Delta AMB\) và \(\Delta DCM\) có: \(\frac{{AB}}{{DM}} = \frac{4}{6} = \frac{6}{9} = \frac{{AM}}{{DC}},\widehat {MAB} = \widehat {MDC} = {90^0}\)

\( \Rightarrow \Delta AMB \backsim \Delta DCM(c - g - c)\)

\( \Rightarrow \widehat {AMB} = \widehat {DCM}\) mà \(\widehat {DMC} + \widehat {DCM} = {90^0}\)

\( \Rightarrow \widehat {AMB} + \widehat {DCM} = {90^0} \Rightarrow \widehat {BMC} = {90^0}\)