Cho hình thang vuông ABCDhat A = hat D = 90^0 có AB = 16cm, — Không quảng cáo

Phương pháp giải

Áp dụng hai tam giác đồng dạng và định lí Pythagore để tính độ dài cạnh BC.

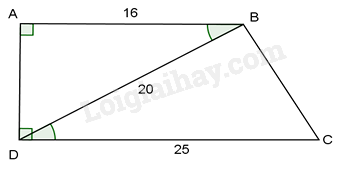
$\Delta ABD$ và $\Delta BDC$ có: $\widehat {ABD} = \widehat {BDC}$ (so le trong, AB//CD)

$\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}$ (Vì $\frac{{16}}{{20}} = \frac{{20}}{{25}})$

Do đó $\Delta ABD \backsim \Delta BDC(c - g - c)$

Ta có ${\rm{\hat A = 90}}{}^0$ nên $\widehat {DBC} = {90^0}$ . Theo định lí Pytago, ta có:

$B{C^2} = C{D^2} - B{D^2} = {25^2} - {20^2} = {15^2}$ .Vậy BC= 15 (cm)