Đề bài
Cho hình thoi ABCD có \(\widehat A\) tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia cạnh đó thành hai đoạn bằng nhau. Tính các góc của hình thoi.
-
A.
\(\widehat B = \widehat D = {80^0},\widehat A = \widehat C = {100^0}\)
-
B.
\(\widehat B = \widehat D = {120^0},\widehat A = \widehat C = {60^0}\)
-
C.
\(\widehat B = \widehat C = {60^0},\widehat A = \widehat D = {120^0}\)
-
D.
\(\widehat B = \widehat D = {60^0},\widehat A = \widehat C = {120^0}\)
Phương pháp giải
Áp dụng tính chất của hình thoi để tính các góc.
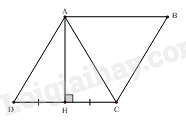
Gọi H là chân đường cao kẻ từ A đến cạnh CD. Từ giả thiết ta có: \(AH \bot CD\), CH = HD suy ra AH là đường trung trực của đoạn CD nên AC = AD (1)
Do ABCD là hình thoi nên AD = CD (2)
Từ (1) và (2) suy ra AD = CD = AC nên \(\Delta ACD\)là tam giác đều, do đó\(\widehat D = {60^0}\).
Vì AB // CD nên \(\widehat {DAB} + \widehat D = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {DAB} = {180^0} - \widehat D = {180^0} - {60^0} = {120^0}\).
Áp dụng tính chất về góc vào hình thoi ABCD ta được: \(\widehat B = \widehat D = {60^0},\widehat A = \widehat C = {120^0}\)
Đáp án : D