Cho hình thoi \(ABCD\) có \(M\) là trung điểm của \(AD\), đường chéo \(AC\) cắt \(BM\) tại điểm \(E\).
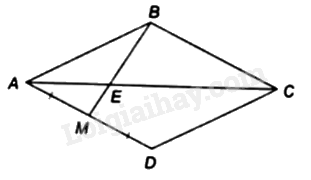
Tỉ số \(\frac{{EM}}{{EB}}\) bằng:
-
A.
\(\frac{1}{3}\)
-
B.
2
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{2}{3}\)
Tính chất của hình thoi (4 cạnh bằng nhau, đường chéo là phân giác của các góc)
Áp dụng tính chất của đường phân giác: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với cạnh kề của hai đoạn ấy.
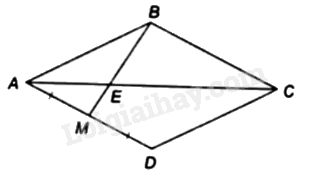
Vì tứ giác \({\rm{ABCD}}\) là hình thoi nên \({\rm{AC}}\) là tia phân giác của \(\widehat {BAD}\) và \(AD = AB\)
Xét \(\Delta ABM\) có \(AE\) là tia phân giác của \(\widehat {BAM}\)
Suy ra \(\frac{{EM}}{{EB}} = \frac{{AM}}{{AB}}\) (tính chất đường phân giác trong tam giác).
Mà \(M\) là trung điểm của \(AD\) nên \(AM = \frac{1}{2}AD = \frac{1}{2}AB\)
Do đó, \(\frac{{EM}}{{EB}} = \frac{{\frac{1}{2}AB}}{{AB}} = \frac{1}{2}\)
Đáp án C.
Đáp án : C