Cho hình vẽ bên, biết \(\widehat {FDC} = 135^\circ ,\widehat {CBx} = 45^\circ ,\)\(\widehat {DCz} = 135^\circ \), \(Dy\parallel Bx,Dy \bot BF\) tại điểm \(F\).
a) Vẽ hình và chứng minh \(Cz\parallel Dy\).
b) Chứng minh \(BC\) là tia phân giác của \(\widehat {FBx}\).
c) Kẻ tia \(Ct\) là tia phân giác của \(\widehat {BCD}\). Chứng minh \(Ct\parallel Dy\).
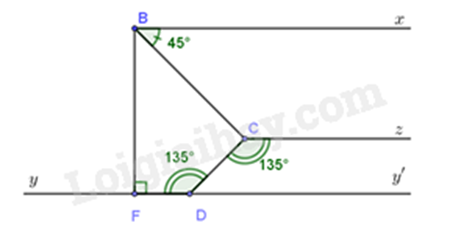
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc so le trong bằng nhau)
b) Chứng minh \(\widehat {FBx} = 90^\circ \).
Chứng minh BC chia góc \(\widehat {FBx}\) thành hai góc bằng nhau.
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Tính được \(\widehat {BCD} = 90^\circ \).
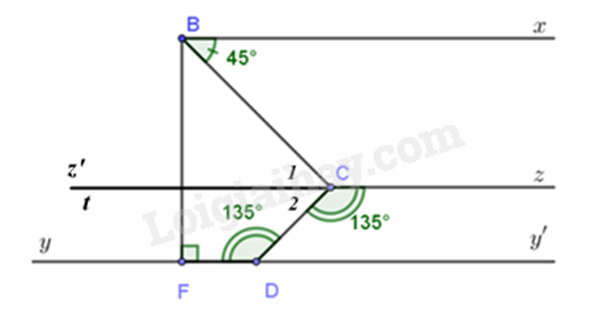
a) Vẽ lại hình
Vì \(\widehat {FDC} = \widehat {DCz} = 135^\circ \) mà \(\widehat {FDC}\) và \(\widehat {DCz}\) ở vị trí so le trong nên \(Cz\parallel Dy\) (dấu hiệu nhận biết)
b) Ta có, \(Dy//Bx;By \bot Dy\) suy ra \(BF \bot Bx\) (tính chất)
Suy ra \(\widehat {FBx} = 90^\circ \)
Tia \(BC\) nằm trong \(\widehat {FBx}\)
Mà \(\widehat {CBx} = \frac{1}{2}\widehat {FBx} = 45^\circ \)
Suy ra\(BC\) là tia phân giác của \(\widehat {FBx}\).
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Khi đó \(Bx//zz'//yy'\)
Suy ra \(\widehat {xBC} = \widehat {{C_1}};\widehat {{C_2}} = \widehat {CDy'}\) (1).
Vì \(\widehat {yDC} + \widehat {CDy'} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CDy'} = 180^\circ - \widehat {yDC} = 180^\circ - 135^\circ = 45^\circ \) (2).
Từ (1) và (2) suy ra \(\widehat {{C_1}} = 45^\circ ;\widehat {{C_2}} = 45^\circ \)
Do đó \(\widehat {BCD} = \widehat {{C_1}} + \widehat {{C_2}} = 45^\circ + 45^\circ = 90^\circ \) \(\)
Vì \(Ct\) là tia phân giác của \(\widehat {BCD}\) nên \(\widehat {DCt} = \frac{1}{2}\widehat {BCD} = 45^\circ \) (tính chất)
Suy ra \(\widehat {DCt} = \widehat {CDy'} = 45^\circ \).
Mà \(\widehat {DCt}\) và \(\widehat {CDy'}\) là hai góc so le trong.
Do đó \(Ct\parallel Dy\) (dấu hiệu nhận biết)