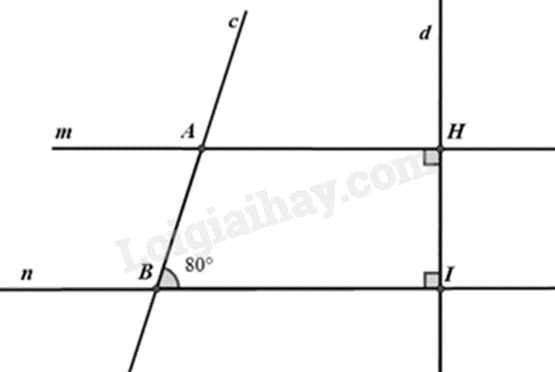
Cho hình vẽ, biết \(\widehat {ABI} = 80^\circ \).
a) Chứng minh \(m//n\).
b) Tính \(\widehat {cAH}\) và \(\widehat {mAc}\).
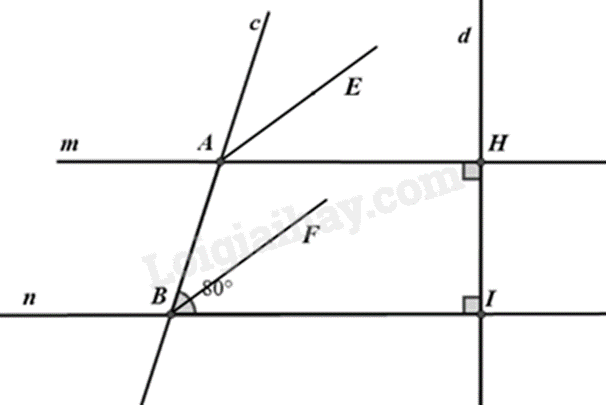
c) Vẽ tia AM là tia phân giác của \(\widehat {cAH}\). Tia BN là tia phân giác của \(\widehat {ABI}\). Chứng minh \(AM//BN\).
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
b) Sử dụng tính chất của hai đường thẳng song song: hai góc đồng vị bằng nhau.
Hai góc kề bù thì tổng của chúng bằng \(180^\circ \).
c) Sử dụng kiến thức về tia phân giác của một góc.
Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc bằng nhau ở vị trí đồng vị)
a) Ta có: \(m \bot d;n \bot d\) nên m // n (tính chất hai đường thẳng song song).
b) Vì m // n nên \(\widehat {cAH} = \widehat {ABI} = 80^\circ \) (hai góc đồng vị).
Vì \(\widehat {mAc}\) và \(\widehat {cAH}\) là hai góc kề bù nên ta có \(\widehat {mAc} + \widehat {cAH} = 180^\circ \)
Suy ra \(\widehat {mAc} = 180^\circ - \widehat {cAH} = 180^\circ - 80^\circ = 100^\circ \).
Vậy \(\widehat {cAH} = 80^\circ ;\widehat {mAc} = 100^\circ \).
c) Vì AE là tia phân giác của \(\widehat {cAH}\) nên \(\widehat {cAE} = \frac{1}{2}\widehat {cAH} = \frac{{80^\circ }}{2} = 40^\circ \).
Tương tự, ta tính được \(\widehat {ABF} = 40^\circ \).
Ta có \(\widehat {cAE} = \widehat {ABF} = 40^\circ \).
Mà hai góc này là hai góc ở vị trí đồng vị nên AE // BF.