Cho hình vẽ, cho biết DE//BC. Khi đó — Không quảng cáo

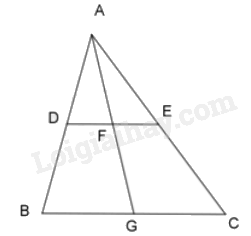
Áp dụng định lí Thales và tính chất bắc cầu để giải bài toán.

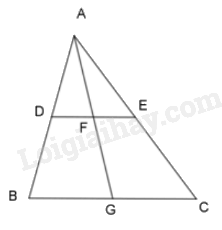
Ta có $DE\parallel BC$ suy ra $DF\parallel BG$ và $FE\parallel GC$

Vì $DF\parallel BG$ áp dụng định lí Thales ta có: $\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}}$ (1)

Vì $FE\parallel GC$ áp dụng định lí Thales ta có: $\frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}$ (2)

Từ (1) và (2) ta có: $\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}$

Đáp án D.