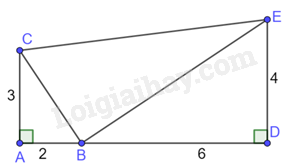
Cho hình vẽ: Chọn đáp án đúng — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ hai của tam giác vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.

Ta có: $\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\frac{{AC}}{{BD}} = \frac{3}{6} = \frac{1}{2}$ nên $\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}$

Tam giác ABC và tam giác DEB có: $\widehat {BAC} = \widehat {BDE} = {90^0},\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}$ nên $\Delta ABC \backsim \Delta DEB$

Do đó, $\widehat {CBA} = \widehat {BED}$

Mà $\widehat {BED} + \widehat {EBD} = {90^0}$ nên $\widehat {ABC} + \widehat {EBD} = {90^0}$

Mà $\widehat {ABC} + \widehat {EBD} + \widehat {CBE} = {180^0}$ nên $\widehat {CBE} = {90^0}$

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có: $B{C^2} = A{B^2} + A{C^2} = 13$

Áp dụng định lý Pythagore vào tam giác BDE vuông tại D có: $B{E^2} = D{E^2} + B{D^2} = 52$

Áp dụng định lý Pythagore vào tam giác BCE vuông tại B có: $C{E^2} = B{E^2} + B{C^2} = 65$ nên $CE = \sqrt {65}$