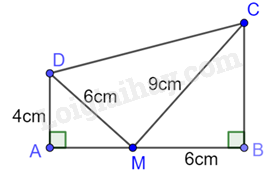
Cho hình vẽ: Chu vi tam giác DMC là — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.

Tam giác ADM và tam giác BMC có:

\(\widehat A = \widehat B = {90^0},\frac{{AD}}{{MB}} = \frac{{DM}}{{MC}}\left( { = \frac{2}{3}} \right)\)

Do đó, \(\Delta AMD \backsim \Delta BCM\) nên \(\widehat {ADM} = \widehat {BMC}\)

Mà: \(\widehat {AMD} + \widehat {ADM} = {90^0},\) do đó, \(\widehat {AMD} + \widehat {BMC} = {90^0}\)

Lại có: \(\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = {180^0}\)

Suy ra: \(\widehat {DMC} = {180^0} - \left( {\widehat {AMD} + \widehat {BMC}} \right) = {90^0}\)

Do đó, tam giác DMC vuông tại M

Áp dụng định lý Pythagore vào tam giác DMC vuông tại M có:

\(D{C^2} = D{M^2} + M{C^2} = 117\) nên \(DC = \sqrt {117} cm\)

Vậy chu vi tam giác DMC là: \(DM + MC + DC = 6 + 9 + \sqrt {117}  = 15 + \sqrt {117} \left( {cm} \right)\)