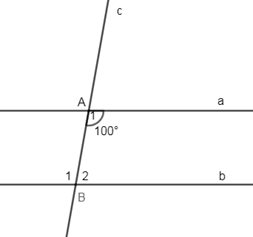
Cho hình vẽ sau, biết \(a//b\) và \(\widehat {{A_1}} = {100^0}\). Tính \(\widehat {{B_1}},\widehat {{B_2}}\).
-
A.
\(\widehat {{B_1}} = \widehat {{B_2}} = {100^0}\)
-
B.
\(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {80^0}\)
-
C.
\(\widehat {{B_1}} = {80^0},\,\,\widehat {{B_2}} = {100^0}\)
-
D.
\(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {90^0}\)
Áp dụng tính chất của hai đường thẳng song song.
Vì \(a//b\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\, = {100^0}\) (hai góc so le trong)
Ta có : \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 100^\circ + \widehat {{B_2}} = 180^\circ \\ \Rightarrow \widehat {{B_2}} = 180^\circ - 100^\circ = 80^\circ \end{array}\)
Đáp án : B