Cho hình vẽ sau:
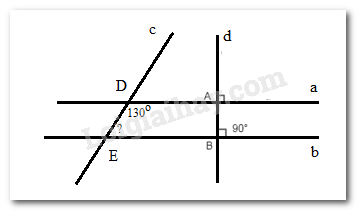
Biết \(a \bot d,\,b \bot d,\,\widehat {A{\rm{D}}E} = {130^0}\). Tính \(\widehat {DEB}\).
-
A.
130\(^\circ \)
-
B.
65\(^\circ \)
-
C.
70\(^\circ \)
-
D.
50\(^\circ \)
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
+ Áp dụng tính chất của 2 đường thẳng song song

Vì \(a \bot d,\,b \bot d\) nên a // b ( Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
Mà \(\widehat {{D_1}} + \widehat {ADE} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{D_1}} + 130^\circ = 180^\circ \\ \Rightarrow \widehat {{D_1}} = 180^\circ - 130^\circ = 50^\circ \end{array}\)
Vì a // b nên \(\widehat {{D_1}} = \widehat {DEB}\) ( 2 góc đồng vị) nên \(\widehat {DEB}\) = 50\(^\circ \)
Đáp án : D