Cho hình vẽ sau, biết \(\widehat {{B_1}} = 40^\circ \), \(\widehat {{C_1}} = 40^\circ \)
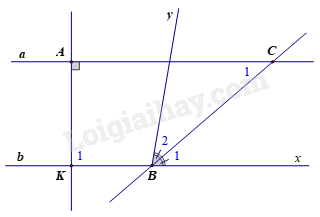
a) Chứng tỏ đường thẳng a song song với đường thẳng b.
b) Tính góc AKB.
c) Cho BC là tia phân giác của góc xBy. Tính góc yBK.
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
b) Hai đường thẳng song song có hai góc so le trong bằng nhau.
c) Sử dụng tính chất tia phân giác và hai góc kề bù.
a) Ta có \(\widehat {{C_1}} = {\widehat B_1} = 40^\circ \) (giả thiết).
Mà \(\widehat {{B_1}}\) và \(\widehat {{C_1}}\) nằm ở vị trí so le trong nên a // b.
b) Vì a // b nên \(\widehat {{K_1}} = \widehat {aAK} = 90^\circ \) (hai góc so le trong).
c) Vì BC là tia phân giác của góc xBy nên \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat {xBy}}}{2} \Rightarrow \widehat {xBy} = {2.40^0} = {80^0}\).
Vì góc xBy và góc yBK là hai góc kề bù nên \(\widehat {xBy} + \widehat {yBK} = {180^0}\)\( \Rightarrow \widehat {yBK} = {180^0} - {80^0} = {100^0}\).